To Memorize: Perbandingan TRIGONOMETRI SOH - CAH - TOA

CLASS X A/B MATIUS : JIA YOU !! SEMANGAT !!

Logika Modus PONENS, TOLENS dan SILOGISME

Soal #1: Modus Ponens
Premis 1 : Jika Budi rajin berolahraga maka badannya sehat.
Premis 2 : Budi rajin berolahraga.

Pembahasan:
Penarikan kesimpulan dengan prinsip Modus Ponens
Modus Ponens
p → q
p
________
∴ q

Jika Budi rajin berolahraga maka badannya sehat.
                     p                                q

Budi rajin berolahraga
              p

Kesimpulan adalah q : Badan Budi sehat
-----------------------------------------------------------------------

Soal #2: Modus Tollens
Tentukan kesimpulan dari :
Premis 1 : Jika hari cerah maka Budi bermain bola.
Premis 2 : Budi tidak bermain bola.

Pembahasan:
p : Hari cerah
q : Budi bermain bola

Penarikan kesimpulan dengan prinsip Modus Tollens
p → q
~q
_______
∴ ~p
Sehingga kesimpulannya adalah " Hari tidak cerah "

---------------------------------------------------------------------------------
Soal #3 Prinsip Silogisme
Tentukan kesimpulan dari :
Premis 1 : Jika Budi rajin belajar maka ia disayang ayah.
Premis 2 : Jika Budi disayang ayah maka ia disayang ibu.

Pembahasan:
Penarikan kesimpulan dengan prinsip silogisme
p → q
q → r
_________
∴ p → r

Sehingga kesimpulannya adalah " Jika Budi rajin belajar maka ia disayang ibu"

---------------------------------------------------------------------------------------
Soal #4:  Prinsip Silogisme
Diketahui premis-premis berikut:
Premis 1 : Jika masyarakat membuang sampah pada tempatnya maka lingkungan bersih.
Premis 2: Jika lingkungan bersih maka hidup akan nyaman.

Kesimpulan yang sah dari kedua premis tersebut adalah…
A. Jika masyarakat membuang sampah pada tempatnya maka hidup akan nyaman.
B. Masyarakat membuang sampah pada tempatnya maka hidup akan nyaman.
C. Jika masyarakat membuang sampah tidak pada tempatnya maka lingkungan tidak akan bersih.
D. Jika masyarakat membuang sampah pada tempatnya maka lingkungan tidak bersih.
E. Masyarakat membuang sampah pada tempatnya tetapi lingkungan tidak bersih.

Pembahasan:
Penarikan kesimpulan. Premisnya berpola silogisme:


Sehingga kesimpulannya adalah “Jika masyarakat membuang sampah pada tempatnya maka hidup akan nyaman.”

-----------------------------------------------------------------------------

English Version of Mathematical Reasoning:

1. Argument Form I

    Given statement 'All A is B' and 'C is A' Then 'C is B'. 

    Premise 1 : All A is B.

    Premise 2 : C is A

    Conclusion: C is B

    Example: 

(i). Make a conclusion based on the two given premises.

     Premise 1: All multiples of 20 are multiples of 5

     Premise 2: 60 is a multiple of 20.

     Conclusion: 60 is a multiple of 5.   

(ii). Make a conclusion based on the two given premises.

      Premise 1: All Girls like Justin Bieber.

      Premise 2: Aurel is a girl.

      Conclusion: Aurel like Justin Bieber.

2. Argument Form II

    Given the implication 'if p, then q' and the statement that p is true. Then q is true.

    Premise 1 :  if p, then q

    Premise 2 : p is true

    Conclusion: q is true

Example: 

(i). Make a conclusion based on the two given premises.

     Premise 1: If a pyramid has a base area of 20 cm2 and a height of 9 cm, then the volume of
     the pyramid is 60 cm3.

     Premise 2: The pyramid VABCD has a base area of 20 cm2 and a height of 9 cm.

     Solution: The volume of the pyramid VABCD is 60 cm3.

(ii). Make a conclusion based on the two given premises.

      Premise 1 : If dilligent then must got A score.

      Premise 2 : Chaca is dilligent student.

      Solution : Chaca will get A score.

3. Argument Form III

    Given the implication 'if p, then q' and the statement that 'not q' is true.Then 'not p' is true.

    Premise 1 :  if p, then q

    Premise 2 : Not q is true

    Conclusion: Not p is true

 

Example: 

(i). Make a conclusion based on the two given premises below.

     Premise 1 :  if Ayla is Daihatsu sedan cars, then Agya is Toyota sedan cars.

     Premise 2 : Ayla is not the same with Agya

     Conclusion: Daihatsu is not the same with Toyota.

BIODATA PENULIS

BIODATA BUNTORO

Stefanus Buntoro Sutanto lahir di Semarang, Jawa   Tengah. Pada 5 Pebruari 1965. Bergabung dengan Sekolah Kristen Bina Bakti (SMAK-2 BinBak) sejak 2014 sampai sekarang. Pada awalnya bertugas sebagai guru matematika kelas IX dan kelas X IPA dan X IPS. 

Buntoro menyelesaikan kuliahnya di dua perguruan tinggi, untuk program D-3 jurusan teknik Mesin Produksi di Politeknik Universitas Diponegoro Semarang tahun 1986. Kemudian program S-1 nya dari Universitas Brawijaya, Malang tahun 1994, jurusan Konstruksi Mesin yang diambilnya tahun 1991 atas program beasiswa dari PT. Dirgantara Indonesia (d/h IPTN). 

Selepas meraih gelar sarjananya ia sempat mengikuti program pembuatan mobil nasional “Maleo” di Melbourne, Australia tahun 1996.

 5 tahun selepas menyelesaikan ikatan dinasnya tahun 2006, ia mengundurkan diri

 dengan hormat dari PT. Dirgantara Indonesia (d/h. IPTN), perusahaan tempat ia 

 sudah mengabdi selama 20 tahun. 

Setelah itu ia banyak merantau dan menimba pengalaman di luar negeri seperti 

di Australia, Jerman dan Malaysia. 

Setelah 7 tahun merantau, baru tahun 2014 kembali ke tanah air dan membaktikan

tenaga dan pikirannya untuk mendidik generasi muda Indonesia khususnya remaja.

Buntoro memiliki pengalaman berorganisasi antara lain sebagai anggota Resimen Mahasiswa UNDIP (1983), Ketua pelaksana kegiatan Pecinta Alam Politeknik (1986), Peserta Training Pilot Ground School CESSNA (1988), ketua pelaksana kegiatan KKMK-Bandung (1989), Wakil RT08/16 kelurahan Margahayu Selatan (2000)  dan Wakil ketua lingkungan St.Lidwina, gereja Martinus-Kopo  (2000).  Saat ini, ia mengajar di SMAK Bina Bakti Bandung, SMP Harapan Kasih dan Home Schooling Cambridge IGCSE.  

Buntoro menikah dengan Veronica dan dikaruniai dua anak,

Ariel Milka Pratama (1995) dan Maria Lidwina Milka Dwiyani (1997). 

Saat ini mereka tengah menyelesaikan studinya di bidang Perhotelan dan Kedokteran Hewan.  

Konsep Sudut ELEVASI dan DEPRESI

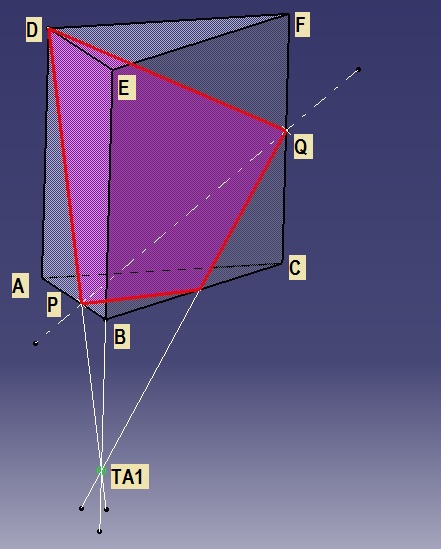
Studi kasus #3: Soal PENAMPANG Prisma Segitiga ( Right Prism Intersection Cut)

Soal Prisma: 

Sebuah prisma ABC.DEF dipotong oleh garis PQ. lukiskan penampang yang melalui titik D, memotong BC dan PQ.

   

Solusi: 

Langkah Penyelesaian:

1. Dari  titik D tarik garis ketitik P, potongkan dengan perpanjangan 

    garis EB sehingga didapatkan titik TA1.

2. Dari titik TA1 tarik garis ke titik Q.

3. Hubungkan garis perpotongan yang merupakan garis tepi 

    penampang (garis merah).

4. Bidang penampang adalah bidang berwarna ungu. 

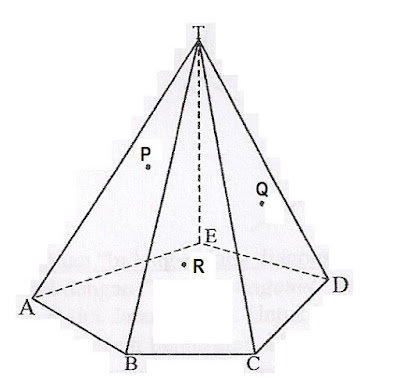
Studi kasus #2: Soal PENAMPANG Limas ( Right Pyramid Intersection Cut)

 Soal Limas: 

Sebuah limas T.ABCDE mempunyai titik potong pada titik P,Q dan R. P pada TAE, Q pada TBC dan R pada TED.

Temukan penampang irisannya dengan menggunakan garis-garis konstruksi.

   Solusi: 

Langkah Penyelesaian:
1. Buat letak P,Q &R menjadi tertentu dengan menarik garis dari 
    puncak limas TK, TL & TM.
2. Tarik garis P ke Q dan K ke L yang berpotongan di TA1.
3.  Tarik garis P ke R dan K ke M yang berpotongan di TA2.
4. Hubungkan titik TA1 dan TA2 untuk mendapatkan Garis afinitas 
    (garis tebal warna hijau) dibidang dasar. 
5. Potongkan perpanjangan garis CD, BC, AB dan ED terhadap 
    garis affinitas sehingga berturut-turut didapat titik 1, 2, 3 & 4.
6. Dari titik perpotongan 1,2,3,4 bisa ditarik kebidang masing-
    masing untuk mendapatkan garis tepi bidang penampang.
7. Hubungkan titik sudut yang didapat sehingga terbentuk bidang 
    penampang warna ungu.

Studi kasus #1: Soal PENAMPANG Kubus (Cuboid Intersection Cut)

Soal Cuboid: 

Sebuah kubus mempunyai titik potong pada titik P,Q dan R.

Temukan penampang irisannya dengan menggunakan garis konstruksi. 

  Solusi: 

Langkah Penyelesaian:
1. Tarik garis dari titik P dan titik R, potongkan dengan garis bidang 
    dasar AB.
    sehingga didapat titik afinitas TA2.
2. Tarik garis dari titik Q dan titik R, potongkan dengan garis    
     bidang dasar CD sehingga didapat titik afinitas TA1.
3. Hubungkan garis melalui titik TA1 dan TA2, ini disebut garis 
    Afinitas (warna hijau). 
4. Potongkan garis bidang dasar AD dengan garis afinitas, didapat 
    titik 4 dan tarik melalui titik P sehingga memotong di titik 6.
5. Potongkan garis bidang dasar CD dengan garis afinitas, didapat
    titik 5 dan tarik melalui titik Q sehingga memotong di titik 7.
6. Hubungkan titik sudut yang didapat sehingga terbentuk bidang 
    penampang warna ungu.

To Memorize: Perbandingan Segitiga ISTIMEWA 45 dan 60 derajat (Asal-Usul Nilai TABEL)

To Memorize: Sudut ISTIMEWA & sudut BERELASI

3D - Study Case #3_Menghitung Jarak

Studi Kasus #3:

Diketahui limas beraturan T.ABCD dengan ABCD adalah persegi yang memiliki panjang AB = 4 cm dan TA = 6 cm. Hitung Jarak titik C ke garis AT.
A. 1/14 √14 cm
B. 2/3 √14 cm
C. 3/4 √14 cm
D. 4/3 √14 cm
E. 3/2 √14 cm

Pembahasan:

Dengan pythagoras dapat ditentukan panjang AC, 

 

dan juga tinggi limas TP 

 

 
Akhirnya dari segitiga ACT diperoleh nilai x:

3D - Study Case #2_Menghitung Jarak

Studi Kasus #2
Pada kubus ABCD.EFGH dengan panjang rusuk 6 cm, jarak titik B ke 

diagonal ruang AG adalah...
A. √5
B. 2√5
C. 3√5
D. 2√6
E. 3√6


Pembahasan:
Misalkan jaraknya adalah BP, dimana BP dengan AG harus tegak lurus. 

Ambil segitiga ABG sebagai acuan perhitungan. Jika AB dijadikan alas 

segitiga, maka BG menjadi tingginya. Jika AG yang dijadikan alas, 

maka tinggi segitiganya adalah BP, dimana BP itulah yang dicari. 

alas_1 x tinggi_1 = alas_2 x tinggi_2

3D - Study Case #1_Menghitung Jarak

Studi Kasus #1

1. Pada kubus ABCD.EFGH, panjang rusuk 8 cm.

    Jarak titik E ke bidang BDG adalah...

    A. 1/3 √3 cm

    B. 2/3 √3 cm

    C. 4/3 √3 cm

    D. 8/3 √3 cm

    E. 16/3 √3 cm

 Pembahasan:
 Perhatikan gambar berikut. Posisi titik E dan bidang BDG 

Garis merah adalah jarak yang akan dicari, dimana garis tersebut harus tegak lurus dengan
bidang BDG. Tambahkan garis-garis bantu untuk mempermudah 

Perhatikan segitiga EQG yang akan digunakan sebagai acuan perhitungan. 

Panjang-panjang yang diperlukan adalah
PQ = 8 cm, sama panjang dengan rusuk kubus.
EG = 8√2 cm, diagonal bidang kubus.
Mencari panjang GQ dengan phytagoras, dengan QC adalah setengah dari diagonal sisi = 4√2 

Kemudian pada segitiga EPQ berlaku 

Kesimpulan:  ER tidak lain adalah jarak titik E ke bidang BGD.